Ultimately, I want you to be able to look at a given series and quickly identify whether it converges or diverges. There will always be some problems that you have to stop and think about, but most should be pretty clear once you're comfortable with the p-series test ideas, the geometric series ratio test and upcoming - a sort of "hierarchy" of functions.
We talked some today about the theory of how you could prove that since the series Sum(1/n^2) converges (p-series test, p = 2), then the series Sum(1/(n^2 + 1)) also converges. The "+1" in the denominator is unimportant for very large values of n so it should basically behave like Sum(1/n^2). Either comparison test - direct comparison (where we note that term by term, 1 / n^2 is greater than 1 / (n^2 + 1) so the sum of 1 / n^2 will also be greater) or limit comparison (take the limit as n -> ∞ of the ratio of the terms and get a positive (finite) value ) would work.
Further notes from today are below.
Tuesday, March 27, 2012
March 26 - p-Series Test
We talked about several things today - the highlights were using an (improper) integral to argue that the series 1 + 1/2 + 1/3 + 1/4 + ... + 1/n + ... diverges and then generalizing to any sum of the form:
Sum(1 / n^p) as n goes from 1 to ∞.
Basically, if p ≤ 1, the series diverges. If p > 1, the series converges.
Notes below.
Sum(1 / n^p) as n goes from 1 to ∞.
Basically, if p ≤ 1, the series diverges. If p > 1, the series converges.
Notes below.
Friday, March 23, 2012
Mar 23 - Improper Integrals
We started today with a look back at the Fundamental Theorem of Calculus. I noted that the FTOC applies to continuous functions on a closed interval [a, b]. Certain integrals will be called "improper" b/c we'll be "violating" one of those conditions. Either we will look at an integral that is discontinuous (typically an asymptote) or an interval that is not bounded - [a, ∞) or (-∞, b].
Mostly we just worked some examples in class. Having to write lim as b -> ∞ over and over gets a little old but it's necessary. Notes from class are below.
Mostly we just worked some examples in class. Having to write lim as b -> ∞ over and over gets a little old but it's necessary. Notes from class are below.
Thursday, March 22, 2012
Mar 21 - Introduction to Series
We talked about series today. A series means "an infinite sum, something of the form a + b + c + ..." with the dot, dot, dot implying that the pattern continues forever.
Determining the behavior of a series will be the fundamental problem of the next two weeks. We'll learn a variety of tests to explain that the sum is findable (the series converges) or that the sum is not findable (the series diverges). Today's two main ideas are the geometric series and the behavior of the nth term.
We did geometric series last year. Identify the constant ratio for the series as r and then if | r |< 1, the series converges. Easy.
The nth term should be mostly intuitive. If I say what is the sum of "2 + 2 + 2 + ..." you would recognize that the sum will continue to increase and thus goes to infinity (the series diverges). The nth term test says that if the limit of the terms in the series aren't approaching 0, then the series diverges.
Note that we don't get to say that if the terms are approaching 0, then the series converges. Turns out that's not necessarily true. Stay tuned.
Notes from today are below.
Determining the behavior of a series will be the fundamental problem of the next two weeks. We'll learn a variety of tests to explain that the sum is findable (the series converges) or that the sum is not findable (the series diverges). Today's two main ideas are the geometric series and the behavior of the nth term.
We did geometric series last year. Identify the constant ratio for the series as r and then if | r |< 1, the series converges. Easy.
The nth term should be mostly intuitive. If I say what is the sum of "2 + 2 + 2 + ..." you would recognize that the sum will continue to increase and thus goes to infinity (the series diverges). The nth term test says that if the limit of the terms in the series aren't approaching 0, then the series diverges.
Note that we don't get to say that if the terms are approaching 0, then the series converges. Turns out that's not necessarily true. Stay tuned.
Notes from today are below.
Wednesday, March 21, 2012
Mar 20 - Sequences
Today (the first day after spring break...) we begin our last new unit. Ultimately, the question we are going to be solving is:
Does the given infinite sum converge?
That's it. Note that in the case of a geometric series, you already know how to answer the question (check the constant ratio) as that was covered in PreCalculus. For the next couple weeks, we'll be studying different arguments for different types of series.
The focus for today is sequences and the main issue is finding the limit of the sequence. In many cases, you already know how to do this b/c it's simply the limit as x-> ∞ that we've already done. The expressions will typically be a little more complicated (involving factorials or combinations of functions for example) and so your thinking will often have to be more nuanced.
The one new tool you'll need is called L'Hospital's Rule. It is used to evaluate limits and applies when direct substitution yields an indeterminate limit of the form 0/0 or ∞/∞.
Notes and examples from today are below.
Does the given infinite sum converge?
That's it. Note that in the case of a geometric series, you already know how to answer the question (check the constant ratio) as that was covered in PreCalculus. For the next couple weeks, we'll be studying different arguments for different types of series.
The focus for today is sequences and the main issue is finding the limit of the sequence. In many cases, you already know how to do this b/c it's simply the limit as x-> ∞ that we've already done. The expressions will typically be a little more complicated (involving factorials or combinations of functions for example) and so your thinking will often have to be more nuanced.
The one new tool you'll need is called L'Hospital's Rule. It is used to evaluate limits and applies when direct substitution yields an indeterminate limit of the form 0/0 or ∞/∞.
Notes and examples from today are below.
Thursday, February 16, 2012
Feb 16 - Arc Length
The main topic for today was finding the length of a curve (given either with parametric equations or as y as a function of x). The fundamental idea is pretty easy (Pythagorean Theorem!) with some algebra tricks thrown in to make the formula an integral.
Unfortunately, while it's a pretty cool topic - most of the integrals generated are ridiculously tough to evaluate. Almost always, you have a square root and it involves something more complicated than a linear function. So for these types of problems, expect to have to just set up the integral (or be allowed to use the calculator to find a numerical answer).
Notes from class are below.
Unfortunately, while it's a pretty cool topic - most of the integrals generated are ridiculously tough to evaluate. Almost always, you have a square root and it involves something more complicated than a linear function. So for these types of problems, expect to have to just set up the integral (or be allowed to use the calculator to find a numerical answer).
Notes from class are below.
Tuesday, February 14, 2012
Feb 14 - Parametric Equations (Slope)
Today we talked about finding the slope of a curve defined by parametric equations. The formula for dy/dx in parametric is a consequence of the Chain Rule and should feel fairly intuitive:
dy/dx = (dy/dt) / (dx/dt)
We worked a couple examples, revisiting the basic derivative questions of finding the slope, writing the equation of a tangent line or determining where a graph might have horizontal or vertical tangent lines. Notice that while it is comfortable having an idea of what the graph looks like, it's not generally necessary to our work.
Notes are posted below.
dy/dx = (dy/dt) / (dx/dt)
We worked a couple examples, revisiting the basic derivative questions of finding the slope, writing the equation of a tangent line or determining where a graph might have horizontal or vertical tangent lines. Notice that while it is comfortable having an idea of what the graph looks like, it's not generally necessary to our work.
Notes are posted below.
Monday, February 13, 2012
Feb 13 - Parametric Equations
We worked a couple problems from the worksheet prior to the quiz. I'll reiterate that ultimately, you will only be responsible for having the Taylor series for e^x, cos x, and sin x memorized. No others need to be memorized.
I spent most of class today _playing_ mathematics. I hope students who were in class got a good feel for how weird and abstract and cool pure mathematics can be and how new and different ways to represent concepts can provide deeper understanding. Unfortunately, I didn't have any real notes for class prepared so I don't have anything to scan in tonight. But I'll update it tomorrow.
We are starting parametric equations (with calculus) tomorrow. There is a short assignment tonight - just using your calculator to generate some graphs.
I spent most of class today _playing_ mathematics. I hope students who were in class got a good feel for how weird and abstract and cool pure mathematics can be and how new and different ways to represent concepts can provide deeper understanding. Unfortunately, I didn't have any real notes for class prepared so I don't have anything to scan in tonight. But I'll update it tomorrow.
We are starting parametric equations (with calculus) tomorrow. There is a short assignment tonight - just using your calculator to generate some graphs.
Wednesday, February 8, 2012
Feb 8 - Taylor Series (Geometric Series)
Today was our second day of finding Taylor series for functions. We
focused on special rational functions that we could treat as
representing the sum of a geometric series. The sum formula we're
building on from last year in Pre-Calculus is:
Sum of infinite geometric series = 1st term / (1 - ratio),
with the condition that the | ratio | < 1.
We worked a couple examples - mostly this is just some arithmetic and algebra.
Notes from today are below.
Sum of infinite geometric series = 1st term / (1 - ratio),
with the condition that the | ratio | < 1.
We worked a couple examples - mostly this is just some arithmetic and algebra.
Notes from today are below.
Tuesday, February 7, 2012
Feb 7 - Taylor Series
Today was an introduction to the idea of a Taylor Series. The general
idea of a Taylor Series is that we are going to take functions and
represent them as "infinite" polynomials. The "Why?" question will be
answered eventually but for now we're going to focus on the "How?"
question.
Most of the Taylor Series we will work with will have the form:
a0 + a1*x + a2*x^2 + a3*x^3 + ... + an*x^n + ...
where each of the coefficients has the form an = f^n(0) / n! (where f^n(0) means "the nth derivative of f(x) evaluated at x = 0).
Generally, a Taylor Series has the form:
a0 + a1*(x - c) + a2*(x - c)^2 + a3*(x - c)^3 + ... + an*(x - c)^n + ...
where each of the coefficients has the form an = f^n(c) / n!
You will eventually be responsible for the Taylor series for e^x, sin x and cos x.
Here is the animation I used in class to illustrate the Taylor series for sin x.
Notes from today are below.
Most of the Taylor Series we will work with will have the form:
a0 + a1*x + a2*x^2 + a3*x^3 + ... + an*x^n + ...
where each of the coefficients has the form an = f^n(0) / n! (where f^n(0) means "the nth derivative of f(x) evaluated at x = 0).
Generally, a Taylor Series has the form:
a0 + a1*(x - c) + a2*(x - c)^2 + a3*(x - c)^3 + ... + an*(x - c)^n + ...
where each of the coefficients has the form an = f^n(c) / n!
You will eventually be responsible for the Taylor series for e^x, sin x and cos x.
Here is the animation I used in class to illustrate the Taylor series for sin x.
Notes from today are below.
 | |
| p1 |
 | |
| p2 |
Feb 6 - Integration
The main goal today was to get practice evaluating integrals. With all the techniques we now have to use, finding antiderivatives can become a very tough exercise and recognizing which technique to use when will take time and patience.
We worked several examples in class. The assignment for tomorrow will be one of the most challenging of the semester. :0
Notes from today are below.

We worked several examples in class. The assignment for tomorrow will be one of the most challenging of the semester. :0
Notes from today are below.

Friday, February 3, 2012
Feb 3 - Integration by Partial Fractions
So this is a very algebra-intensive concept. It's a technique for finding antiderivatives of rational functions. Generally, you want to try our other techniques before resorting to partial fractions.
Conceivably, the polynomial in the denominator might have a quadratic factor (x^3 - 8 factoring into (x - 2)(x^2 + 2x + 4)) or a repeated factor (x^3 - 2x^2 + x factoring into x(x - 1)^2). In these instances, the algebra of solving the partial fractions is a bit more challenging but as it turns out, we will not have to worry about those cases in BC Calculus. Simple, non-repeated linear terms are the only partial fractions problems we'll see according to the BC curriculum from The College Board.
(If we had "extra" days for instruction - this is the kind of thing I might spend another day on...)
We worked a couple examples in class. One thing to remember is that partial fractions only works if the denominator of the rational function is greater than that of the numerator. If the degrees are the same (or the top is greater), then there is division to be done.
Notes are below.
p1

p2

Conceivably, the polynomial in the denominator might have a quadratic factor (x^3 - 8 factoring into (x - 2)(x^2 + 2x + 4)) or a repeated factor (x^3 - 2x^2 + x factoring into x(x - 1)^2). In these instances, the algebra of solving the partial fractions is a bit more challenging but as it turns out, we will not have to worry about those cases in BC Calculus. Simple, non-repeated linear terms are the only partial fractions problems we'll see according to the BC curriculum from The College Board.
(If we had "extra" days for instruction - this is the kind of thing I might spend another day on...)
We worked a couple examples in class. One thing to remember is that partial fractions only works if the denominator of the rational function is greater than that of the numerator. If the degrees are the same (or the top is greater), then there is division to be done.
Notes are below.
p1

p2

Thursday, February 2, 2012
Feb 2 - Integration by Parts
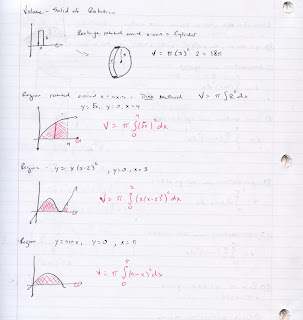
Yesterday most of classtime was dedicated to working on a volume worksheet - taking the same region, R, and creating a variety of solids.
Today, we learned the first of two new integration techniques for the week. It is called integration by parts and has the basic rule:
Integral of u*dv = u*v - Integral of v*du
It is based on the formula used for the product of functions (the Product Rule).
My thought process is that once I've decided that an integral can't be done by substitution, I'll try integration by parts. The first step for me is to determine "dv." Essentially, dv should be the "most complicated" part of the integral that I can integrate easily. "u" is whatever is leftover.
We worked several examples in class. Notes from class are below.
p1

p2

Today, we learned the first of two new integration techniques for the week. It is called integration by parts and has the basic rule:
Integral of u*dv = u*v - Integral of v*du
It is based on the formula used for the product of functions (the Product Rule).
My thought process is that once I've decided that an integral can't be done by substitution, I'll try integration by parts. The first step for me is to determine "dv." Essentially, dv should be the "most complicated" part of the integral that I can integrate easily. "u" is whatever is leftover.
We worked several examples in class. Notes from class are below.
p1

p2

Tuesday, January 31, 2012
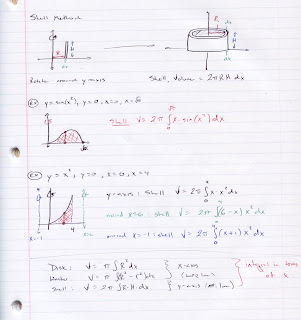
Jan 31 - Volume problems
We went over the homework from last night and then had a quiz over the shell method.
We derived the formula for finding the volume of a cone in class by taking a triangular region in the first quadrant and rotating it around each axis. The notes I'm posting show the work for finding the volume of a specific cone (intercepts of (0, 4) and (2, 0)) though in class we used variables R and H for the intercepts.
My notes from class are below.

We derived the formula for finding the volume of a cone in class by taking a triangular region in the first quadrant and rotating it around each axis. The notes I'm posting show the work for finding the volume of a specific cone (intercepts of (0, 4) and (2, 0)) though in class we used variables R and H for the intercepts.
My notes from class are below.

Monday, January 30, 2012
Jan 30 - Volume of a Solid of Rotation (Shell)
To this point, we've been rotating around the x-axis and other horizontal lines. Today we'll look at solids generated by rotating around the y-axis (and other vertical lines).
I think this problem is a little more difficult for students because we're not "stacking" shapes (circles, washers, squares, triangles, etc) to create solids. Moreover the surface we're using (called a shell) is not a planar shape, so you have to do a little more work imagining.
The basic idea is that a rectangle rotated around a vertical axis creates the following shape.
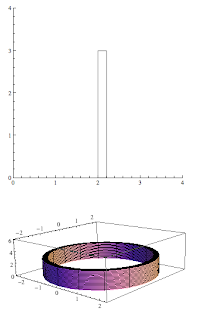
A shell _is_ washer-like, but we're calling it something different because what we're making infinitesimal is different. That's an important distinction. For a washer, it's height is dx. For this shape, the width of the shell (between in the inner and outer walls) is dx. The formula for the volume of this shape will be analogous to finding the lateral surface area of a cylinder. We will have
V = 2π*R*H*dx
Notes from class (including a couple of examples):
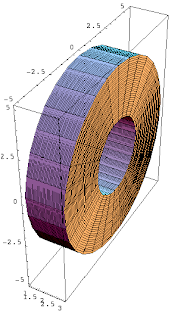
I think this problem is a little more difficult for students because we're not "stacking" shapes (circles, washers, squares, triangles, etc) to create solids. Moreover the surface we're using (called a shell) is not a planar shape, so you have to do a little more work imagining.
The basic idea is that a rectangle rotated around a vertical axis creates the following shape.

A shell _is_ washer-like, but we're calling it something different because what we're making infinitesimal is different. That's an important distinction. For a washer, it's height is dx. For this shape, the width of the shell (between in the inner and outer walls) is dx. The formula for the volume of this shape will be analogous to finding the lateral surface area of a cylinder. We will have
V = 2π*R*H*dx
Notes from class (including a couple of examples):

Friday, January 27, 2012
Jan 27 - Volume of Solid of Rotation (Washer)
There is a lot of similarity between yesterday's lesson and today's. In both cases, we are rotating regions in the xy-plane around a horizontal line. Yesterday, we looked at situations where we were rotating around one of the boundaries of the region (often the x-axis). Today we will discuss rotating regions around horizontal lines in general.
The geometry problem that relates here is this - given that there are two concentric circles, one with a radius of 5 and the other with a radius of 2, find the area of the purple region in between them.

The calculation to find that purple area isn't particularly difficult:
π(5)^2 - π(2)^2 = 25π - 4π = 21π
Most calculus students feel comfortable with this idea. Recognize though that we never worried about the fact that the "radius" of that purple area is 3 - it never comes into play.
When you rotate a rectangle around one of it's edges, you get a disk (cylinder). When you rotate a rectangle around a line that is not an edge, you get a solid that we will call a washer. Note that it is a cylinder with a smaller cylinder removed from the center.
If we take a rectangle with opposite vertices (1, 2) and (2, 5) and rotate it around the x-axis we get the following washer.

Recognize the geometry problem with the purple and gold circles. Finding the volume of the washer is the same idea. We'll use the formula:
V = π(R^2)H - π(r^2)H which simplifies to π(R^2 - r^2)H
So in this case, the volume of the washer is V = π(5^2)(1) - π(2^2)(1) b= 25π - 4π = 21π.
To find volume when we rotate regions around horizontal lines, we'll use
V = π Integral( (R^2 - r^2) dx) where the dx represents the (infinitesimal) height of each washer.
Notes from class today are below.
The geometry problem that relates here is this - given that there are two concentric circles, one with a radius of 5 and the other with a radius of 2, find the area of the purple region in between them.

The calculation to find that purple area isn't particularly difficult:
π(5)^2 - π(2)^2 = 25π - 4π = 21π
Most calculus students feel comfortable with this idea. Recognize though that we never worried about the fact that the "radius" of that purple area is 3 - it never comes into play.
When you rotate a rectangle around one of it's edges, you get a disk (cylinder). When you rotate a rectangle around a line that is not an edge, you get a solid that we will call a washer. Note that it is a cylinder with a smaller cylinder removed from the center.
If we take a rectangle with opposite vertices (1, 2) and (2, 5) and rotate it around the x-axis we get the following washer.


Recognize the geometry problem with the purple and gold circles. Finding the volume of the washer is the same idea. We'll use the formula:
V = π(R^2)H - π(r^2)H which simplifies to π(R^2 - r^2)H
So in this case, the volume of the washer is V = π(5^2)(1) - π(2^2)(1) b= 25π - 4π = 21π.
To find volume when we rotate regions around horizontal lines, we'll use
V = π Integral( (R^2 - r^2) dx) where the dx represents the (infinitesimal) height of each washer.
Notes from class today are below.

Thursday, January 26, 2012
Jan 26 - Volume of Solid of Rotation (Disk)
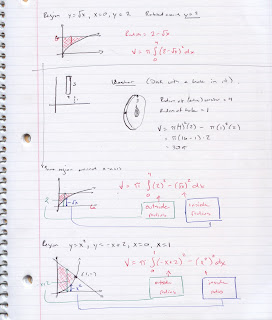
Our second day of volume problems introduces the idea of creating a solid by rotating a region in the xy-plane around a line. Today, we learned the Disk method, so called because of the shape created when a rectangle is rotated around one of its edges.
Recall that when we began talking about integrals, we had the idea of a Riemann Sum. Under certain conditions (f(x) ≥ 0), a Riemann Sum could be interpreted as an area approximation, since each of the products f(x) * ∆x was (by defintion) the area of a rectangle. Make the rectangles narrow enough (∆x -> 0) and the number of rectangles big enough (n -> ∞) and the Riemann Sum turned into the definite integral and was defined to be the area.
Same idea now, except instead of using f(x) * ∆x as the area of a rectangle, we'll use π(f(x))^2 * ∆x to represent the volume of a Disk (essentially volume of a cylinder = π(R^2)H).
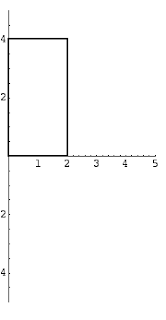
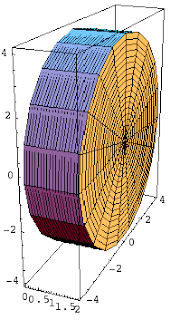
or
Thinking about what we did yesterday, if we can identify the cross-section of the solid, we can create an integral of the form Integral(A(x) dx) where A(x) is the area of the cross-section. Note that when we rotate a region, we create a solid where the cross-sections are all circles. Since the area of a circle is πR^2, all we need to do is figure out what the radius of the cross-section is. In the easiest version of the problem (region is bounded by y = f(x), y = 0 and then some bounds x = a and x = b), the R will be f(x) and so the volume is given by π*Integral( (f(x))^2 dx).
So for example, suppose we have the region bounded by y = Sqrt(x), y = 0 and x = 4. We rotate it around the x-axis to create a solid.
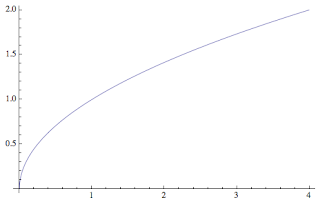
becomes
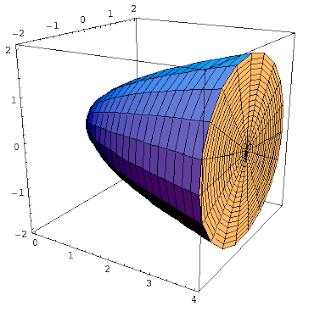
If we imagine approximating the volume using a Riemann Sum (the way we would use a Riemann Sum to approximate the area), we would see something like:
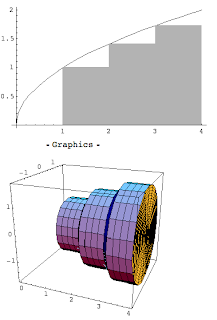
The integral representing the volume of the shape would be π*Integral( (Sqrt(x))^2 dx)
Notes from today are below.
p1
p2

Recall that when we began talking about integrals, we had the idea of a Riemann Sum. Under certain conditions (f(x) ≥ 0), a Riemann Sum could be interpreted as an area approximation, since each of the products f(x) * ∆x was (by defintion) the area of a rectangle. Make the rectangles narrow enough (∆x -> 0) and the number of rectangles big enough (n -> ∞) and the Riemann Sum turned into the definite integral and was defined to be the area.
Same idea now, except instead of using f(x) * ∆x as the area of a rectangle, we'll use π(f(x))^2 * ∆x to represent the volume of a Disk (essentially volume of a cylinder = π(R^2)H).


or
Thinking about what we did yesterday, if we can identify the cross-section of the solid, we can create an integral of the form Integral(A(x) dx) where A(x) is the area of the cross-section. Note that when we rotate a region, we create a solid where the cross-sections are all circles. Since the area of a circle is πR^2, all we need to do is figure out what the radius of the cross-section is. In the easiest version of the problem (region is bounded by y = f(x), y = 0 and then some bounds x = a and x = b), the R will be f(x) and so the volume is given by π*Integral( (f(x))^2 dx).
So for example, suppose we have the region bounded by y = Sqrt(x), y = 0 and x = 4. We rotate it around the x-axis to create a solid.

becomes

If we imagine approximating the volume using a Riemann Sum (the way we would use a Riemann Sum to approximate the area), we would see something like:

The integral representing the volume of the shape would be π*Integral( (Sqrt(x))^2 dx)
Notes from today are below.
p1

p2

Wednesday, January 25, 2012
Jan 25 - Volume Known Cross Section
We began the study of volume problems today. For now, we are generating solids (3D shapes) by defining the base of the solid as some region in the xy-plane and then describing the cross sections of the solid.
For example, suppose I defined the base of some solid as the region bounded by y = sin x, y = 0, x = 0 and x = 2π. If I further stated that the solid had cross sections that were squares, it would look like:
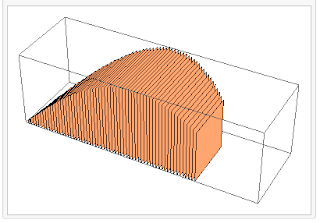
(note that in order to show the cross sections, in this image and in each of the ones that follow I have not "completed" the shape. Above, I've drawn the solid from x = 0 to approximately x = 3π/4).
With the same base, if the cross sections were equilateral triangles, it would look like this:
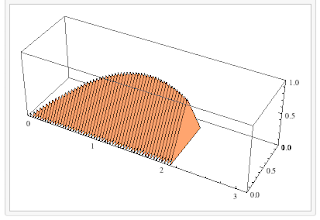
Cross sections of rectangles with constant height = 2 would look like:
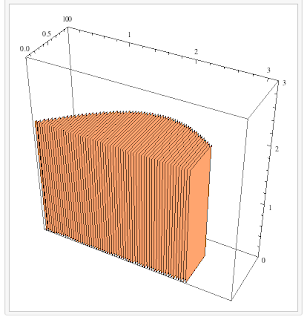
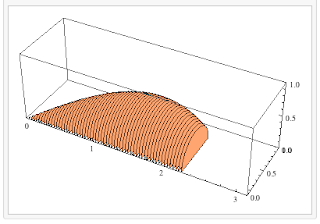
while cross sections of semicircles would look like:
The cool thing is that the "formula" for the volumes of each of these solids is conceptually the same. In all cases, the hard part is representing A(x), the area of the cross section, and in each case, you end up using a formula from geometry. Once you write A(x), the volume is simply given by Integral(A(x) dx) from the lower bound to the upper bound.
Notes from today, including the integration volume formulas for each of the shapes above are included here.

For example, suppose I defined the base of some solid as the region bounded by y = sin x, y = 0, x = 0 and x = 2π. If I further stated that the solid had cross sections that were squares, it would look like:

(note that in order to show the cross sections, in this image and in each of the ones that follow I have not "completed" the shape. Above, I've drawn the solid from x = 0 to approximately x = 3π/4).
With the same base, if the cross sections were equilateral triangles, it would look like this:

Cross sections of rectangles with constant height = 2 would look like:

while cross sections of semicircles would look like:

The cool thing is that the "formula" for the volumes of each of these solids is conceptually the same. In all cases, the hard part is representing A(x), the area of the cross section, and in each case, you end up using a formula from geometry. Once you write A(x), the volume is simply given by Integral(A(x) dx) from the lower bound to the upper bound.
Notes from today, including the integration volume formulas for each of the shapes above are included here.

Tuesday, January 24, 2012
Jan 24 - Area between curves
Today should feel pretty comfortable considering that it's been 7 weeks (less one day) since we've met as a class. (!) It's an application of integration and we've actually calculated areas using integrals already. There will be two new things that you will see. First we'll use two functions as boundaries, rather than having the x-axis always be one of the boundaries, thus the integrals will usually be some Integral((f(x) - g(x)) dx rather than just Integral(f(x) dx). The second new thing will be more complicated and that is that we will occasionally set up integrals with respect to y (instead of x). It shouldn't be more difficult but it always seems to be - it's just kind of bizarre to do things "up/down" rather than "left/right." Fortunately we won't do much of the dy thing.
If you can get yourself believing why the integral works and conceptually understanding what we're doing, then the next week or so will follow well.
Notes from today are attached.
p1
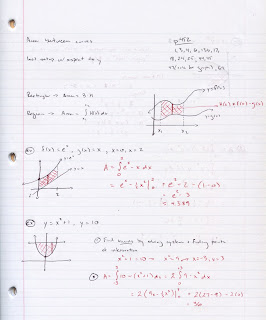
p2

If you can get yourself believing why the integral works and conceptually understanding what we're doing, then the next week or so will follow well.
Notes from today are attached.
p1

p2

Subscribe to:
Comments (Atom)











