Jan 26 - Volume of Solid of Rotation (Disk)

Our second day of volume problems introduces the idea of creating a solid by rotating a region in the xy-plane around a line. Today, we learned the Disk method, so called because of the shape created when a rectangle is rotated around one of its edges.

Recall that when we began talking about integrals, we had the idea of a Riemann Sum. Under certain conditions (f(x) ≥ 0), a Riemann Sum could be interpreted as an area approximation, since each of the products f(x) * ∆x was (by defintion) the area of a rectangle. Make the rectangles narrow enough (∆x -> 0) and the number of rectangles big enough (n -> ∞) and the Riemann Sum turned into the definite integral and was defined to be the area.

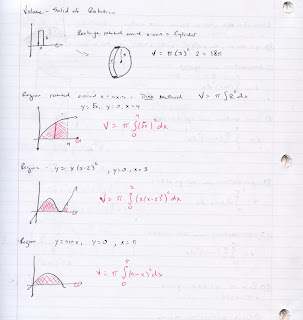
Same idea now, except instead of using f(x) * ∆x as the area of a rectangle, we'll use π(f(x))^2 * ∆x to represent the volume of a Disk (essentially volume of a cylinder = π(R^2)H).


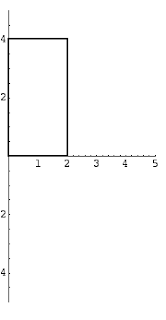
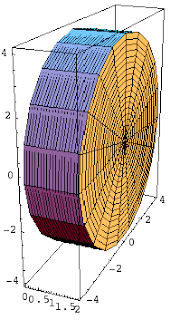
or

Thinking about what we did yesterday, if we can identify the cross-section of the solid, we can create an integral of the form Integral(A(x) dx) where A(x) is the area of the cross-section. Note that when we rotate a region, we create a solid where the cross-sections are all circles. Since the area of a circle is πR^2, all we need to do is figure out what the radius of the cross-section is. In the easiest version of the problem (region is bounded by y = f(x), y = 0 and then some bounds x = a and x = b), the R will be f(x) and so the volume is given by π*Integral( (f(x))^2 dx).

So for example, suppose we have the region bounded by y = Sqrt(x), y = 0 and x = 4. We rotate it around the x-axis to create a solid.


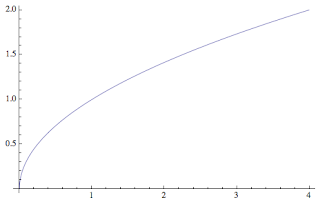
becomes



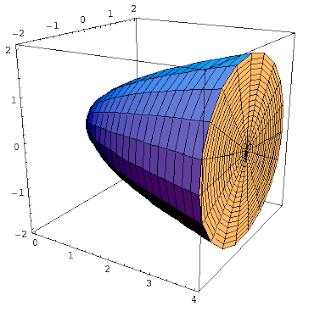
If we imagine approximating the volume using a Riemann Sum (the way we would use a Riemann Sum to approximate the area), we would see something like:



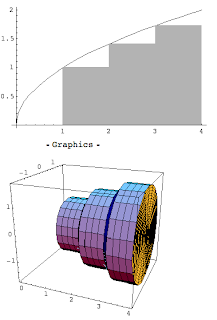
The integral representing the volume of the shape would be π*Integral( (Sqrt(x))^2 dx)

Notes from today are below.

p1


p2