Jan 30 - Volume of a Solid of Rotation (Shell)

To this point, we've been rotating around the x-axis and other horizontal lines. Today we'll look at solids generated by rotating around the y-axis (and other vertical lines).

I think this problem is a little more difficult for students because we're not "stacking" shapes (circles, washers, squares, triangles, etc) to create solids. Moreover the surface we're using (called a shell) is not a planar shape, so you have to do a little more work imagining.

The basic idea is that a rectangle rotated around a vertical axis creates the following shape.


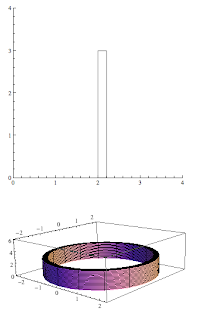
A shell _is_ washer-like, but we're calling it something different because what we're making infinitesimal is different. That's an important distinction. For a washer, it's height is dx. For this shape, the width of the shell (between in the inner and outer walls) is dx. The formula for the volume of this shape will be analogous to finding the lateral surface area of a cylinder. We will have

V = 2π*R*H*dx

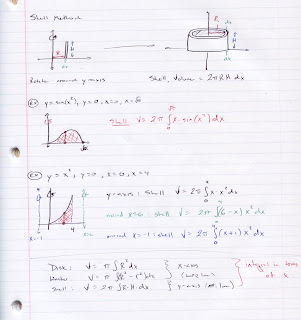
Notes from class (including a couple of examples):