Jan 25 - Volume Known Cross Section

We began the study of volume problems today. For now, we are generating solids (3D shapes) by defining the base of the solid as some region in the xy-plane and then describing the cross sections of the solid.

For example, suppose I defined the base of some solid as the region bounded by y = sin x, y = 0, x = 0 and x = 2π. If I further stated that the solid had cross sections that were squares, it would look like:


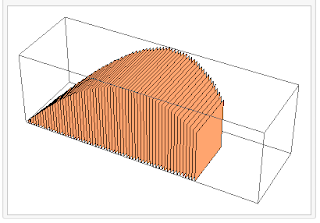
(note that in order to show the cross sections, in this image and in each of the ones that follow I have not "completed" the shape. Above, I've drawn the solid from x = 0 to approximately x = 3π/4).

With the same base, if the cross sections were equilateral triangles, it would look like this:


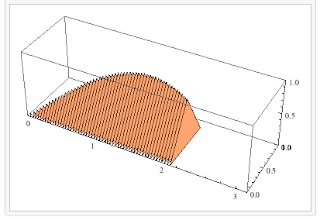
Cross sections of rectangles with constant height = 2 would look like:


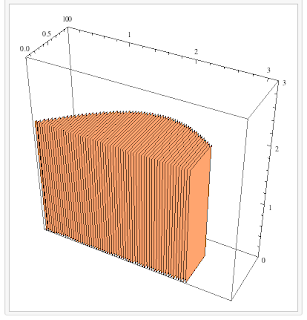
while cross sections of semicircles would look like:


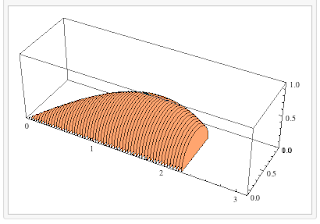
The cool thing is that the "formula" for the volumes of each of these solids is conceptually the same. In all cases, the hard part is representing A(x), the area of the cross section, and in each case, you end up using a formula from geometry. Once you write A(x), the volume is simply given by Integral(A(x) dx) from the lower bound to the upper bound.

Notes from today, including the integration volume formulas for each of the shapes above are included here.