Jan 31 - Volume problems

We went over the homework from last night and then had a quiz over the shell method.

We derived the formula for finding the volume of a cone in class by taking a triangular region in the first quadrant and rotating it around each axis. The notes I'm posting show the work for finding the volume of a specific cone (intercepts of (0, 4) and (2, 0)) though in class we used variables R and H for the intercepts.

My notes from class are below.

Jan 30 - Volume of a Solid of Rotation (Shell)

To this point, we've been rotating around the x-axis and other horizontal lines. Today we'll look at solids generated by rotating around the y-axis (and other vertical lines).

I think this problem is a little more difficult for students because we're not "stacking" shapes (circles, washers, squares, triangles, etc) to create solids. Moreover the surface we're using (called a shell) is not a planar shape, so you have to do a little more work imagining.

The basic idea is that a rectangle rotated around a vertical axis creates the following shape.


A shell _is_ washer-like, but we're calling it something different because what we're making infinitesimal is different. That's an important distinction. For a washer, it's height is dx. For this shape, the width of the shell (between in the inner and outer walls) is dx. The formula for the volume of this shape will be analogous to finding the lateral surface area of a cylinder. We will have

V = 2π*R*H*dx

Notes from class (including a couple of examples):

Jan 27 - Volume of Solid of Rotation (Washer)

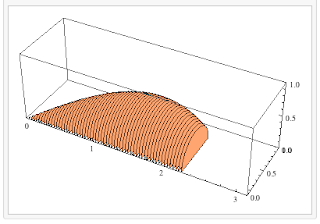
There is a lot of similarity between yesterday's lesson and today's. In both cases, we are rotating regions in the xy-plane around a horizontal line. Yesterday, we looked at situations where we were rotating around one of the boundaries of the region (often the x-axis). Today we will discuss rotating regions around horizontal lines in general.

The geometry problem that relates here is this - given that there are two concentric circles, one with a radius of 5 and the other with a radius of 2, find the area of the purple region in between them.


The calculation to find that purple area isn't particularly difficult:

π(5)^2 - π(2)^2 = 25π - 4π = 21π

Most calculus students feel comfortable with this idea. Recognize though that we never worried about the fact that the "radius" of that purple area is 3 - it never comes into play.

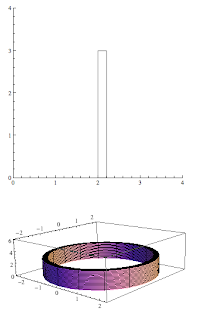
When you rotate a rectangle around one of it's edges, you get a disk (cylinder). When you rotate a rectangle around a line that is not an edge, you get a solid that we will call a washer. Note that it is a cylinder with a smaller cylinder removed from the center.

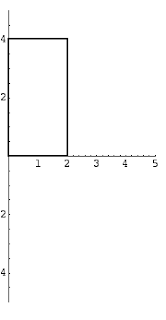
If we take a rectangle with opposite vertices (1, 2) and (2, 5) and rotate it around the x-axis we get the following washer.




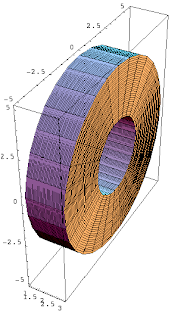
Recognize the geometry problem with the purple and gold circles. Finding the volume of the washer is the same idea. We'll use the formula:

V = π(R^2)H - π(r^2)H which simplifies to π(R^2 - r^2)H

So in this case, the volume of the washer is V = π(5^2)(1) - π(2^2)(1) b= 25π - 4π = 21π.

To find volume when we rotate regions around horizontal lines, we'll use

V = π Integral( (R^2 - r^2) dx) where the dx represents the (infinitesimal) height of each washer.

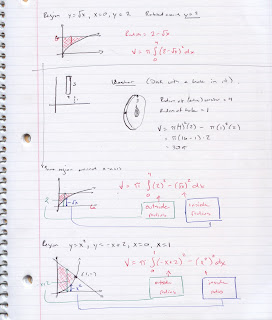
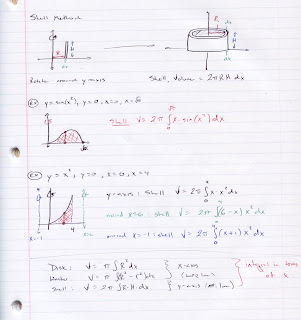
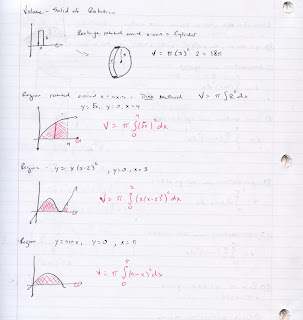
Notes from class today are below.

Jan 26 - Volume of Solid of Rotation (Disk)

Our second day of volume problems introduces the idea of creating a solid by rotating a region in the xy-plane around a line. Today, we learned the Disk method, so called because of the shape created when a rectangle is rotated around one of its edges.

Recall that when we began talking about integrals, we had the idea of a Riemann Sum. Under certain conditions (f(x) ≥ 0), a Riemann Sum could be interpreted as an area approximation, since each of the products f(x) * ∆x was (by defintion) the area of a rectangle. Make the rectangles narrow enough (∆x -> 0) and the number of rectangles big enough (n -> ∞) and the Riemann Sum turned into the definite integral and was defined to be the area.

Same idea now, except instead of using f(x) * ∆x as the area of a rectangle, we'll use π(f(x))^2 * ∆x to represent the volume of a Disk (essentially volume of a cylinder = π(R^2)H).


or

Thinking about what we did yesterday, if we can identify the cross-section of the solid, we can create an integral of the form Integral(A(x) dx) where A(x) is the area of the cross-section. Note that when we rotate a region, we create a solid where the cross-sections are all circles. Since the area of a circle is πR^2, all we need to do is figure out what the radius of the cross-section is. In the easiest version of the problem (region is bounded by y = f(x), y = 0 and then some bounds x = a and x = b), the R will be f(x) and so the volume is given by π*Integral( (f(x))^2 dx).

So for example, suppose we have the region bounded by y = Sqrt(x), y = 0 and x = 4. We rotate it around the x-axis to create a solid.


becomes



If we imagine approximating the volume using a Riemann Sum (the way we would use a Riemann Sum to approximate the area), we would see something like:



The integral representing the volume of the shape would be π*Integral( (Sqrt(x))^2 dx)

Notes from today are below.

p1


p2

Jan 25 - Volume Known Cross Section

We began the study of volume problems today. For now, we are generating solids (3D shapes) by defining the base of the solid as some region in the xy-plane and then describing the cross sections of the solid.

For example, suppose I defined the base of some solid as the region bounded by y = sin x, y = 0, x = 0 and x = 2π. If I further stated that the solid had cross sections that were squares, it would look like:


(note that in order to show the cross sections, in this image and in each of the ones that follow I have not "completed" the shape. Above, I've drawn the solid from x = 0 to approximately x = 3π/4).

With the same base, if the cross sections were equilateral triangles, it would look like this:


Cross sections of rectangles with constant height = 2 would look like:


while cross sections of semicircles would look like:


The cool thing is that the "formula" for the volumes of each of these solids is conceptually the same. In all cases, the hard part is representing A(x), the area of the cross section, and in each case, you end up using a formula from geometry. Once you write A(x), the volume is simply given by Integral(A(x) dx) from the lower bound to the upper bound.

Notes from today, including the integration volume formulas for each of the shapes above are included here.

Jan 24 - Area between curves

Today should feel pretty comfortable considering that it's been 7 weeks (less one day) since we've met as a class. (!) It's an application of integration and we've actually calculated areas using integrals already. There will be two new things that you will see. First we'll use two functions as boundaries, rather than having the x-axis always be one of the boundaries, thus the integrals will usually be some Integral((f(x) - g(x)) dx rather than just Integral(f(x) dx). The second new thing will be more complicated and that is that we will occasionally set up integrals with respect to y (instead of x). It shouldn't be more difficult but it always seems to be - it's just kind of bizarre to do things "up/down" rather than "left/right." Fortunately we won't do much of the dy thing.

If you can get yourself believing why the integral works and conceptually understanding what we're doing, then the next week or so will follow well.

Notes from today are attached.

p1

p2